Solving Weak Acid/Base Dissociation Problems
Dissociation problems are about calculations of hydronium ion concentration, [H3O+], and/or pH of aqueous solutions containing any of the following:
Weak acid and weak base dissociate (or ionize) partially in aqueous solution. Their dissociation products combine to form again the initial weak acid and base.These two reactions occur simultaneously and form an equilibrium. This is in contrast to the strong acids and bases that undergo complete dissociation or ionization in aqueous solution.
Basically, these reactions are about giving up and gaining protons. Those that donate protons are called Bronsted-Lowry acids; and those that accept protons are called Bronsted-Lowry bases.
Their dissociation equilibria given below show that a weak acid loses a proton and forms conjugate base while a weak base gains a proton and forms conjugate acid.
The extent of dissociation (or ionization) is determined by their so called dissociation constants ( Ka for acid and Kb for base ), measured at 25° C.
The dissociation constant is a measure of the tendency of a weak acid to give up a proton and tendency of a weak base to gain a proton. A very small dissociation constant value indicates a very low degree of dissociation.




Values in [ ] denote concentration in moles/liter.
Since the [H2O] in each case is considered constant, it is incorporated into Ka and Kb.
Take note here that water acts as a weak base in weak acid dissociation and acts as a weak acid in weak base dissociation. A solvent that can act either as an acid or as a base depending upon the solute is called amphiprotic ( or amphoteric ) solvent.

The following discussion is about the calculations of hydronium ion concentration of the aqueous solutions containing (a) a weak acid or a weak base, (b) a strong acid or a strong base, (c) a salt of a weak acid or a salt of a weak base, and (d) a weak acid and its salt or a weak base and its salt.
A. Aqueous Solution of a Weak Acid or a Weak Base
The [H3O+] and/or pH of this solution can be calculated using equations 1 and 2.
Since the amount (or concentration) of dissociated acid or base is equal to the amount (or concentration) of dissociation products:
[dissociated acid] = [H3O+] = [A-] = x, and
[ionized base] = [BH+] = [OH-] = x, then
we can set equations 1 and 2 to one unknown:

Equations 3 and 4 have the general form of ax2 + bx + c = 0 which can be solved by using the quadratic equation:

If the dissociation constant value is very low such that x is negligible, the following approximation can be made:

If the dissociation constant value or % error is high, equations 3 and 4 should then be used for calculation.


B. Aqueous Solution of a Strong Acid or a Strong Base
At 25° C, water has the following dissociation equilibrium:


Since [H2O] is considered constant, it is incorporated into Kw.
Kw is called the ion-product constant of water at 25° C. This means that pure water has this much amount dissociated at this temperature, that is, [H3O+] = [OH-] = 1 x 10-7 M. The [H3O+] or [OH-] of an aqueous solution can be calculated when one of them is known.
Addition of a strong acid or base in water will shift the equilibrium to the left, as predicted by Le Chatelier principle, lowering the [H3O+] and [OH-] by depressing the dissociation of water.


Since a strong acid or base dissociates completely in water, then:
[acid] = [H3O+]
[base] = [OH-]
So,

Setting equation 7 to one unknown:
[dissociated water] = [H3O+] = [OH-] = x
1 x 10-14 = ( [acid or base] + x )( x )
which can be solved by using quadratic equation.
But x is very small, we can assume that:

The sample problem below shows the validity of our assumption that x is negligible.


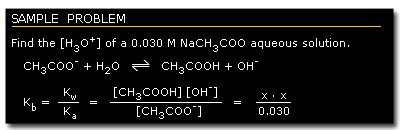
C. Aqueous Solution of a Salt of a Weak Acid or a Salt of a Weak Base
Salt of a weak acid dissociates completely in water as Na+ and A-.
A-, as a conjugate base of HA, reacts with water to form the following equilibrium:

Multiplying Ka (equation 1) by Kb, we get:

Equation 8 indicates the relationship that the strength of a weak acid or base tends to increase as the strength of its conjugate pair decreases, or vice versa.
This equation enables us to compute the dissociation constant value of the conjugate base of a weak acid and the conjugate acid of a weak base, as well as the [H3O+] of this solution.

D. Aqueous Solution of a Weak Acid And Its Salt or a Weak Base And Its Salt
An aqueous solution containing a weak acid and its salt (or a weak base and its salt) is called a buffered solution or simply buffer solution. This is so because a buffer solution's hydronium ion concentration changes very little upon its dilution or upon addition of a strong acid/base.
The changes in pH value are so small such that the pH of the solution remains practically constant.
Calculation of the buffer solution's pH involves the use of equation 1 or 2:
By taking the negative logarithm of each term of the rearranged equation 1, we get equation 9 which is known as the Henderson-Hasselbach equation.

This equation is commonly used for pH calculation in biochemistry problems.


Problems
The best way to improve your problem solving skill in chemistry is to practice solving as many chemistry problems as possible. Try solving the following problems.
Problems are solved using approximation and the quadratic equation. Values in parenthesis are obtained using the quadratic equation.
For more problems on this topic and other chemistry topics, go to www.tutorpartner.blogspot.com.
| 1. | Calculate the dissociation constant of the conjugate base of HC2H2ClO2. Ka = 1.36 x 10-3. |
| Answer: 7.35 x 10-12 | |
| 2. | A one liter aqueous solution contains 9.54 g KOH. What is the pH of this solution? The dissociation constant for water, Kw, is 1 x 10-14. ( KOH = 56.1056 g ) |
| Answer: pH = 13.23 | |
| 3. | An aqueous solution has a strength of 0.05 M HOCN and 0.07 M NaOCN. Calculate the pH of this solution. ( Ka = 3.3 x 10-4) |
| Answer: pH = 3.63 ( 3.63 ) | |
| 4. | Calculate the pH of a 0.3 M NaC6H5O solution. (Ka for phenol acid is 1.05 x 10-10; Kw = 1 x 10-14) |
| Answer: pH = 11.73 ( 11.72 ) | |
| 5. | 110 mL of 0.01 M NaOH solution is added to 110 mL of 0.11 M HNO2 solution. Find the pH of the resulting solution. Given: Ka for nitrous acid is 4.5 x 10-4. |
| Answer: pH = 2.35 ( 2.56) | |
| 6. | A one liter aqueous solution contains 9.2 g NaOH. What is the pH of this solution? The dissociation constant for water, Kw, is 1 x 10-14. ( NaOH = 39.99707 g ) |
| Answer: pH = 13.36 | |
| 7. | What is the pH of an aqueous solution having a concentration of 0.07 M HOCN and 0.02 M NaOCN? ( Ka = 3.3 x 10-4) |
| Answer: pH = 2.94 ( 2.97 ) | |
| 8. | If a solution of HOCN has a concentration of 0.9 M, what is its pH? Ka for cyanic acid is 3.3 x 10-4. |
| Answer: pH = 1.76 ( 1.77 ) | |
| 9. | Find the pH of a 0.86 M NaC6H5COO solution. (Ka for benzoic acid is 6.3 x 10-5; Kw = 1 x 10-14) |
| Answer: pH = 9.07 ( 9.07 ) | |
| 10. | An aqueous solution of 0.12 M CH3COOH and 0.12 M NaCH3COO has a volume of 340 mL. If 1.6 g of NaOH is added to this solution, find the change in pH. Assume no change in the volume of solution. ( Ka = 1.8 x 10-5; NaOH = 39.99707 g ) |
| Answer: pH = 6.75 ( 6.75) | |
| 11. | What is the pH of a solution of 0.28 M NaCH3COO? Calculate the percent hydrolysis. (Ka = 1.8 x 10-5; Kw = 1 x 10-14) |
| Answer: pH = 9.1; 4.45 x 10-3 % ( 9.1; 4.45 x 10-3 % ) | |
| 12. | What is the pH of an aqueous solution of 0.09 M C6H5NH3Cl? ( Given: Kb = 3.94 x 10-10; Kw = 1 x 10-14) |
| Answer: pH = 2.82 ( 2.82 ) | |
| 13. | If 3 L of 0.01 M HOC2H4NH2 solution has a pH of 10.37, find the weight of HOC2H4NH3Cl dissolved in the solution. ( Kb for ethanolamine is 3.18 x 10-5; mol. wt. = 97.5443 ) |
| Answer: 0.4 g | |
| 14. | In a buffer solution of 0.07 M HC2H2ClO2 and 0.07 M NaC2H2ClO2, HCl is added to it such that its calculated concentration in the solution is 0.02 M. Assuming a constant volume of solution, find the change in pH of the solution. ( Ka = 1.36 x 10-3) |
| Answer: pH = 2.61 ( 2.64 ) | |
| 15. | Find the [H+] and [OH-] of a 0.24 M of HF solution. Ka = 6.7 x 10-4; Kw = 1 x 10-14. |
| Answer: [H+] = 1.27 x 10-2 M; [OH-] = 7.89 x 10-13 M ( 1.24 x 10-2; 8.1 x 10-13 ) | |
| 16. | What is the dissociation constant of the conjugate acid of HOC2H4NH2. Kb = 3.18 x 10-5. |
| Answer: 3.14 x 10-10 | |
| 17. | What is the pH of a 0.38 M CH3COOH solution. ( Ka = 1.8 x 10-5 ) |
| Answer: pH = 2.58; ( 2.58) | |
| 18. | What is the pH of an aqueous solution of NH2C2H4NH2 having a concentration of 0.01 M? The dissociation constant of ethylenediamine is 8.5 x 10-5. |
| Answer: pH = 10.96 ( 10.94) | |